Imagina que tienes 1/2 (un medio) de una barra de chocolate 🍫 y un amigo te regala 1/2 (un medio) más. La suma de fracciones nos ayuda a saber cuánta barra tienes en total, en este caso 2/2 (dos medios), que es equivalente a 1/1 de una barra de chocolate 🍫 😀.
Cuando sumas fracciones, el proceso se trata de combinar partes de ese entero o todo 🧩, como en el ejemplo anterior.
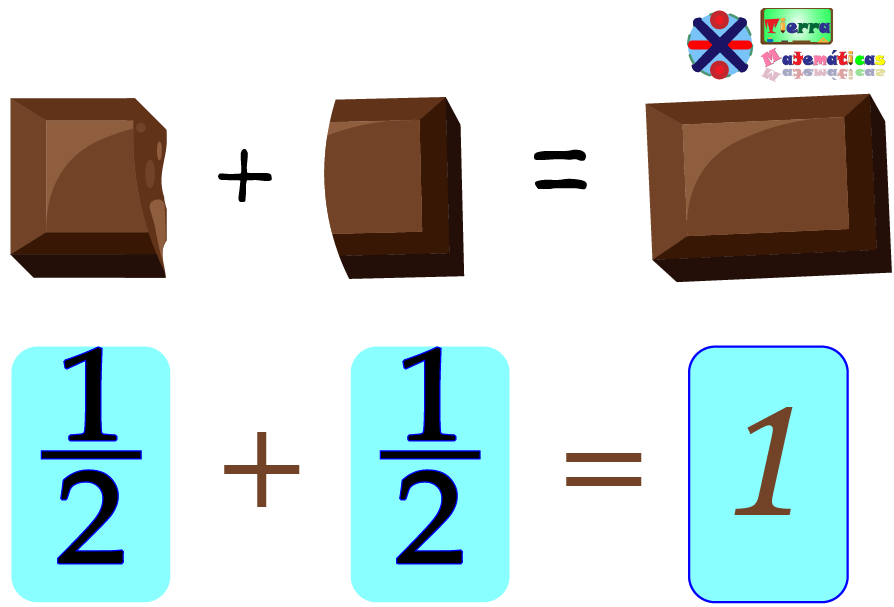
Para que la suma funcione, las fracciones deben ser divididas por la misma cantidad, o en otras palabras, el mismo denominador. Aquí es donde la idea de un denominador común se vuelve importante.
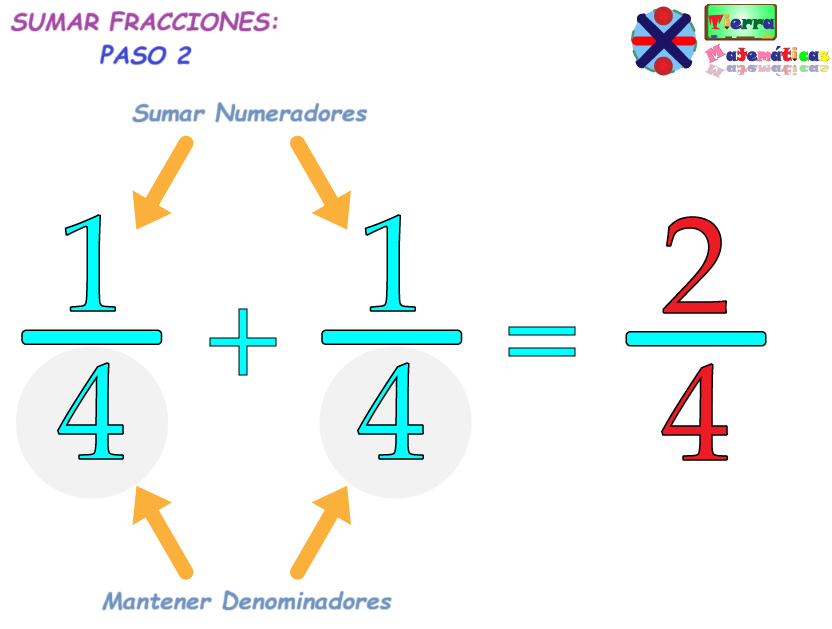
El denominador común es el número que ambos denominadores (los números de que se encuentran en la parte inferior) de dos o más fracciones comparten. Por ejemplo, ¼ + ¼.
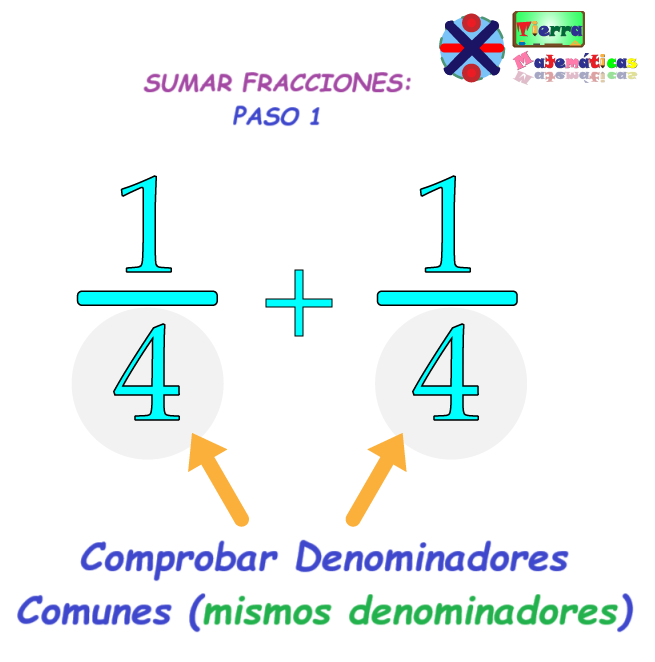
Dado que ambas fracciones comparten el mismo denominador, simplemente podemos sumar los numeradores (los números que se encuentran en la parte superior) y mantener los denominadores.
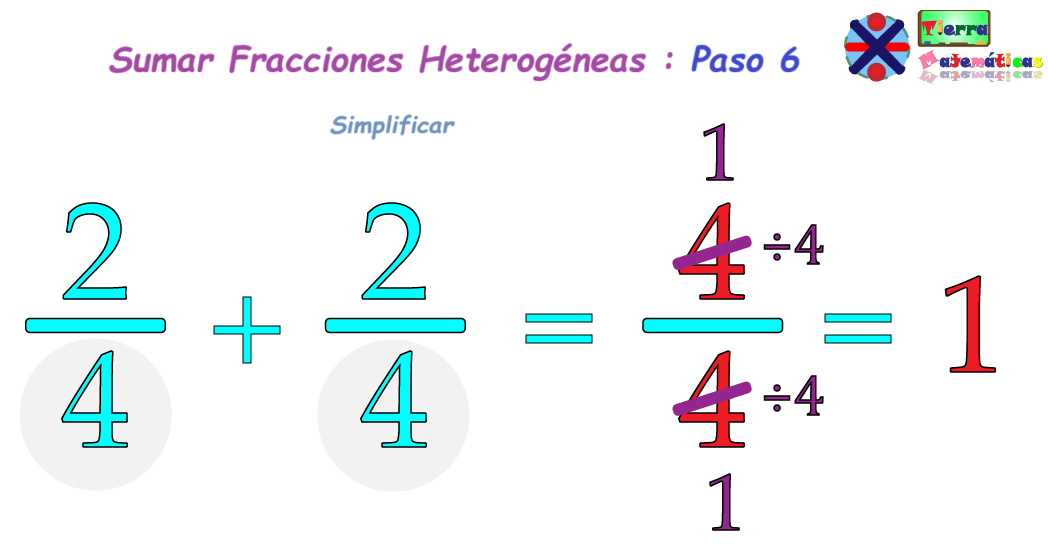
Después de sumar las fracciones, el siguiente paso es chequear si el resultado obtenido es simplificable.
Simplificar una fracción es basicamente reducirla a su forma más sencilla, y es aquí dónde debemos aprender qué es el Máximo Común Divisor (MCD).
Para simplificar una fracción, usa el MCD, para reducirla a su forma más simple.
El MCD es el número más grande que divide sin dejar residuo al numerador y al denominador. Por ejemplo, en la fracción 2/4, tanto el numerador como el denominador pueden ser divididos por 1 y 2.
Debido a que 2 es el mayor de estos dos números, elegimos 2 como el máximo común divisor y dividimos tanto el numerador como el denominador por 2.

Las fracciones heterogéneas tienen denominadores distintos, lo que significa que los números que se encuentran en la parte de abajo de las fracciones no son iguales.


Cuando sumamos o restamos fracciones y nos encontramos con fracciones heterogéneas, necesitamos buscar un denominador común antes de poder combinarlas.
Podemos encontrar este denominador común usando el mínimo común múltiplo (MCM).
El MCM es el número más pequeño que ambos denominadores comparten.
Para hallar el MCM, escribe los múltiplos de cada número (denominador) — en este caso, los múltiplos son 4 y 2, y busca los que se repitan.
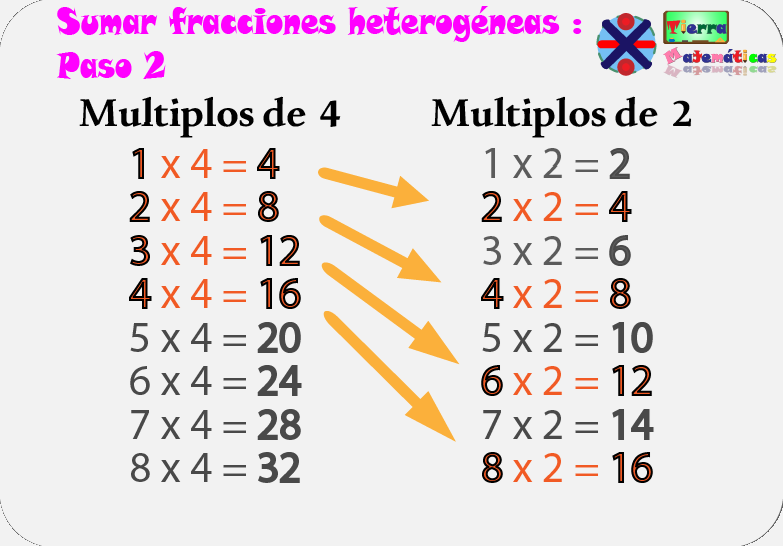
Acá hemos encontrado los múltiplos más cercanos que ambos números tienen en común:
Múltiplos de 4
4, 8, 12, 16, etc.
Múltiplos de 2
4, 8, 12, 16, etc.
Después de tener la lista de los múltiplos que 4 y 2 tienen en común, nos damos cuenta que el número más pequeño o más cercano que aparece en ambas listas es 4, así que 4 es el MCM.
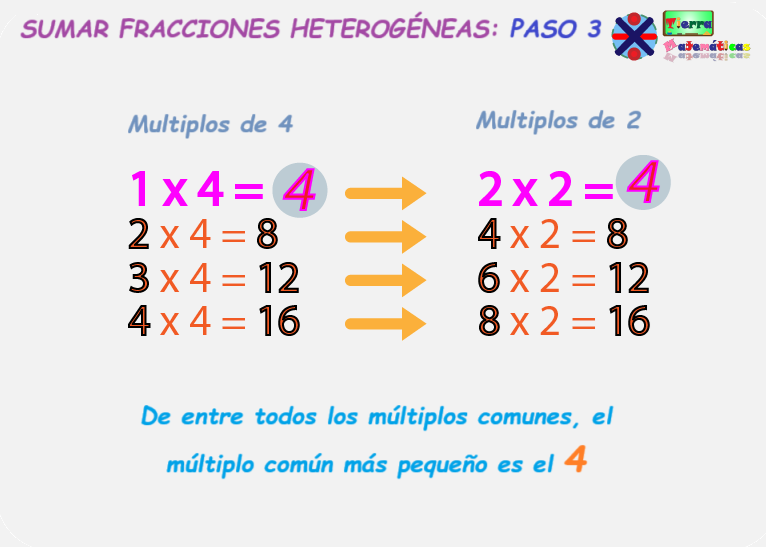
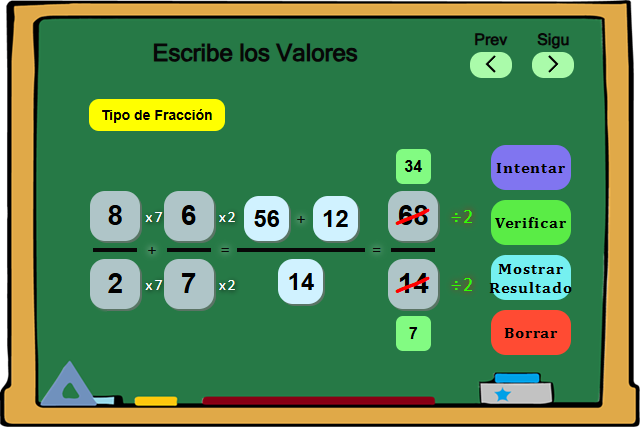
Una vez que tenemos el MCM que habíamos buscado, que es 4, necesitamos reescribir ambas fracciones para que esta vez tengan el mismo denominador.
En este caso, para hacer que los denominadores sean iguales, multiplicamos el primer denominador (4) por 1, para llegar al MCM (4), y luego multiplicamos el segundo denominador (2) por 2 para llegar al mismo MCM (4).
También debemos multiplicar el primer numerador (2) por 1, y el segundo numerador (1) por 2 para hacer que ambas fracciones sean equivalentes.

Después de convertir las fracciones al mismo denominador, solo suma los numeradores y conserva el denominador.

¿Recuerdas que el M.C.D es el número más grande que puede dividir de manera exacta tanto el numerador como el denominador de una fracción? Por ejemplo, en la fracción 4/4, tanto el numerador como el denominador pueden ser divididos por 1, 2 y 4.
Dado que 4 es el más grande de estos tres números, elegimos 4 como el máximo común divisor y dividimos
tanto el numerador como el denominador por 4.
Cuando dividimos tanto el numerador como el denominador por 4, obtenemos
1/1, que puede ser simplemente 1.