La división es una forma de compartir o dividir cosas en partes iguales.
Nos ayuda a descubrir cuántas veces un número cabe en otro o a cómo dividir un grupo de elementos de manera equitativa entre personas.

La división te dice cuántos grupos iguales puedes hacer a partir de una cantidad total.
Abajo hay algunos ejemplos que te ayudarán a comprender mejor el proceso para dividir.
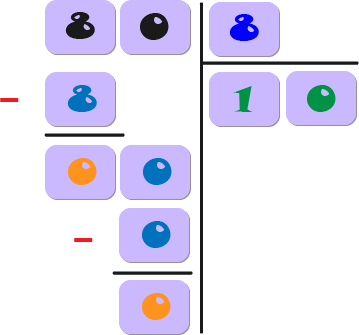
A veces, cuando divides, puedes tener algunos residuos o restos. Por ejemplo,
- Imagina que tienes 10 galletas
- Compartes las galletas con 3 amigos. Empiezas dándole una galleta a cada amigo
- Cada amigo tomaría 3 galletas, dejándote con 1 galleta que no encaja de manera uniforme en los grupos.
- Esta galleta sobrante se llama el residuo o resto.
- Entonces, con la división intentas crear partes iguales, pero no siempre lo haces perfectamente, y lo que queda es un residuo.
- Imagina que estás en una fiesta con 8 de tus amigos. Hay 1 pastel en la fiesta, y quieres compartirlo igualmente con todos.
- Quieres dividir 1 pastel entero igualmente entre las 8 personas. Para hacer eso, cortas el pastel en pedazos más pequeños.
- Como hay 8 personas, cortas el pastel en 8 piezas iguales. Cada persona recibirá una pieza.
- 1 pastel entero ÷ 8 personas = 1/8 de pastel por persona. Entonces, cada persona recibe un pedazo que es 1/8 del pastel entero.
La división es una forma de dividir las cosas de manera equitativa. La usas para cortar el pastel en pedazos más pequeños, ¡así cada persona recibe la misma cantidad!
Puedes practicar división aquí con esta pizarra de dividir.
Hay varios métodos para resolver divisiones largas, pero nos esfocaremos en los estilos Europeos y Americanos.
Ambos métodos llegan al mismo resultado, pero varían en la forma en que se presentan y en ciertos detalles procedimentales.
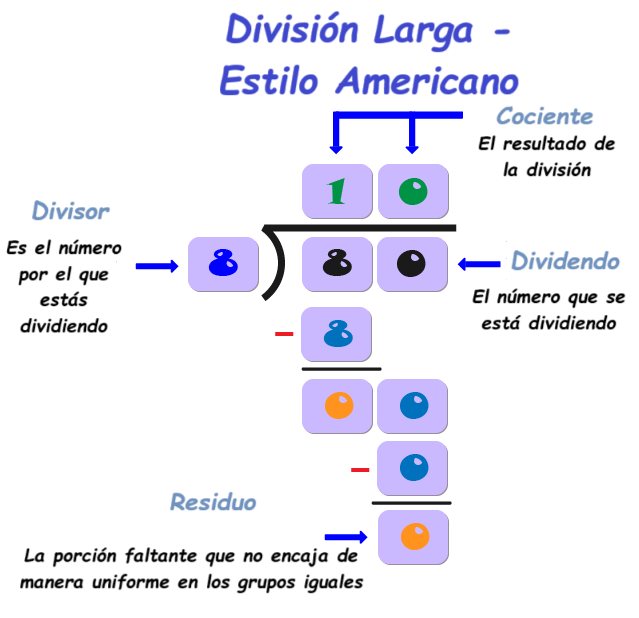
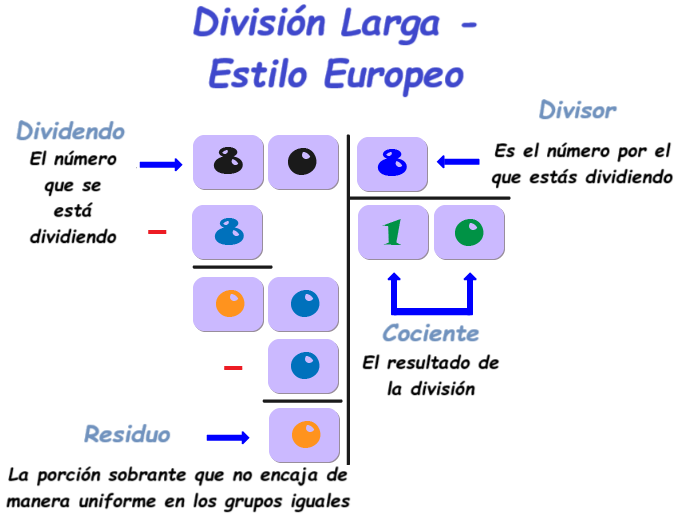
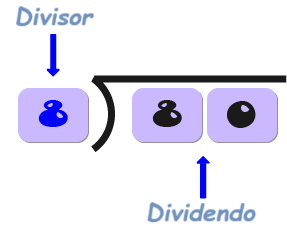
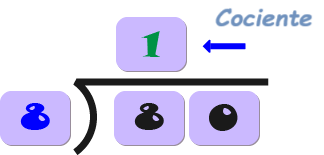
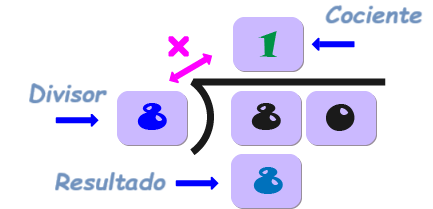
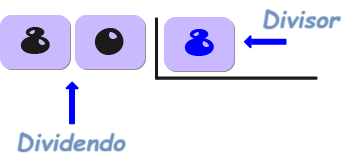
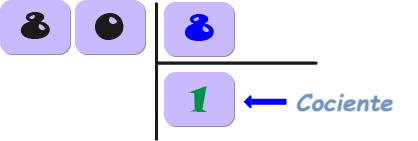
Las partes de la división son el divisor, el dividendo y el cociente, y también el residuo.
Es el número por el que estás dividiendo.
Es el número que se está dividiendo.
El resultado de la división.
La porción sobrante que no encaja de manera uniforme en los grupos iguales.
Resolver problemas de división depende de la complejidad de la división. Por ejemplo, cuando trabajamos con números simples, podemos pensar en la división como una operación opuesta a la de la multiplicación y usar las tablas de multiplicar para resolverlos.
Miremos este ejemplo.
¿Cuánto es 16 dividido por 8?
O digamos, trata de descubrir cuántos grupos de 8 puedes hacer a partir de 16.

La respuesta es 2.

Cada vez que divides un número, básicamente estás preguntando, "¿Qué número multiplicado por el divisor (8) me dará el dividendo (16)?"
Y se demuestra así que la división es solo una multiplicación inversa.

Para este ejemplo, comenzaremos a usar el estilo de división larga americano.
Dividamos 80 entre 8.

1) Mira la primera parte del dividendo (80).
- Determina cuántas veces el divisor (8) cabe en el primer dígito
(8) del dividendo sin excederlo.
O pregúntate "¿Qué número multiplicado por el divisor (8) me dará el primer dígito del dividendo (8) sin excederlo?"
2) El número que multiplicado por el divisor (8) me dio el primer dígito del dividendo (8) es (1), porque (1 x 8 (divisor) = 8 (primer dígito del dividendo)).
- Escribe ese número (1) encima de la barra de división como parte del cociente.
3) Multiplica el divisor (8) por el cociente (1) que acabas de calcular.
- Escribe este resultado (8 x 1 = 8) debajo del dígito del dividendo (8) con el que acabas de trabajar.
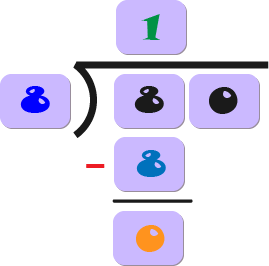
4) Resta el resultado de la multiplicación (8 x 1 = 8) del dígito que estabas considerando, en este caso el primer dígito del dividendo (8).
Escribe la diferencia de (8 - 8 = 0) debajo.
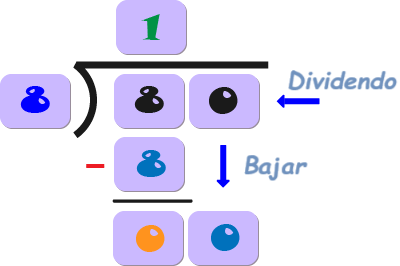
5) Baja el siguiente dígito del dividendo (0) junto a la diferencia que acabas de calcular (0).
6) Repetimos el proceso encontrando qué número multiplicado por el divisor (8) dará el siguiente dígito del dividendo (0).
En este caso, ( (divisor) 8 x 0 = 0 (segundo dígito del dividendo)).
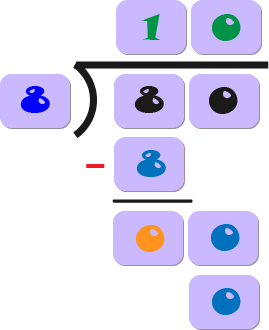
7) Y luego restamos el resultado del segundo dígito del dividendo que acabamos de bajar (0), y escribimos la diferencia (0 - 0 = 0) debajo.
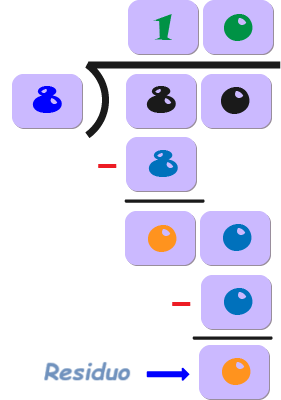
Si al final de la resta obtienes un número más pequeño que el divisor (8), ese número es el resto.
Dado que no hay más dígitos para bajar y el resto es 0, la respuesta final (cociente) es 10.
Y es así cómo se resuelven divisiones usando el estilo americano 😊
Usa nuestra pizarra de divisiones para dominar el proceso de la división larga utilizando el estilo americano y el estilo europeo.
Para el siguiente ejemplo, utilizaremos el estilo de división larga europeo.
Vamos a dividir 80 entre 8.

1) Veamos a la primera parte del dividendo ( 80 ).
- Descubre cuántas veces el divisor (8) puede caber en el primer dígito (8) del dividendo sin excederlo. Alternativamente, puedes preguntarte, "¿Qué número multiplicado por el divisor (8) será igual al primer dígito del dividendo (8) sin excederlo?"
2) El número que, al multiplicarse por el divisor (8), iguala al primer dígito del dividendo (8) es (1), ya que (1 x 8 = 8). Pon ese número (1) debajo de la barra de división como parte del cociente.
3) Multiplica el divisor (8) por el cociente (1) que acabas de calcular.
- Escribe el resultado (8 x 1 = 8) debajo del dígito del dividendo (8) con el que acabas de trabajar.
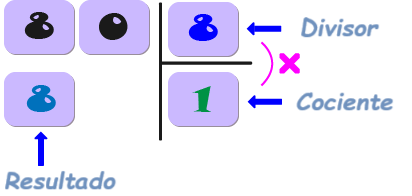
4) Resta el resultado de la multiplicación (8 x 1 = 8) del dígito que estabas considerando, que es el primer dígito del dividendo (8). -Escribe la diferencia de (8 - 8 = 0) debajo.
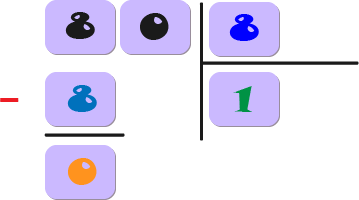
5) Baja el siguiente dígito del dividendo (0) y colócalo junto a la diferencia que acabas de calcular (0).
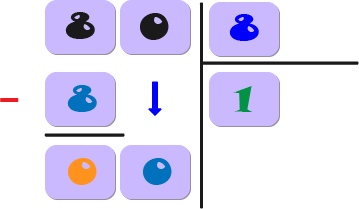
6) Repetimos el proceso encontrando qué número multiplicado por el divisor (8) dará el siguiente dígito del dividendo (0). En este caso, (divisor) 8 x 0 = 0 (segundo dígito del dividendo).
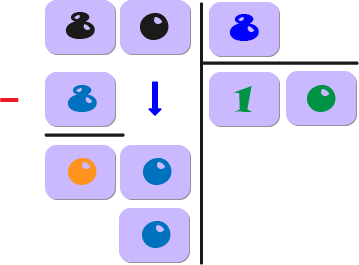
7) A continuación, resta el resultado del segundo dígito del dividendo que acabamos de bajar (0), y escribimos la diferencia (0 - 0 = 0) debajo.